Trong các bảng công thức, thì công thức tính diện tích và chu vi hình tam giác là một trong những bảng công thức cực kỳ khó nhớ và có rất nhiều trường hợp khác nhau để áp dụng công thức.
Tuy nhiên, các công thức này lại áp dụng trong khá nhiều trường hợp và nhiều bài tập khác nhau. Cùng với ThaoTruong, đi xét một số trường hợp cụ thể khác nhau để tính diện tích và chu vi hình tam giác cho thật chuẩn để các bạn nhỏ áp dụng làm bài tập.
Các loại tam giác trong toán học
Trong toán học, thì chúng ta thường gặp 8 loại tam giác như sau:
Tam giác thường
- Là loại tam giác cơ bản nhất, có số đo các cạnh và số đo các góc bằng nhau cũng là loại tam giác thường gặp nhất trong toán học.
Tam giác cân
- Là tam giác có hai cạnh bằng nhau, hai cạnh này được gọi là hai cạnh bên. Đỉnh của một tam giác cân là giao điểm của hai cạnh bên.
Tam giác đều
- Là trường hợp đặc biệt của tam giác cân có cả ba cạnh bằng nhau. Và có 3 góc bằng nhau và bằng 60 độ.
Tam giác vuông
- Là tam giác có một góc bằng 90 độ (là góc vuông).
Tam giác tù
- Là tam giác có một góc trong lớn hơn lớn hơn 90 độ (một góc tù) hay có một góc ngoài bé hơn 90 độ (một góc nhọn).
Tam giác nhọn
- Là tam giác có ba góc trong đều nhỏ hơn 90 độ (ba góc nhọn) hay có tất cả góc ngoài lớn hơn 90 độ (sáu góc tù).
Tam giác vuông cân
- Là loại tam giác vừa là tam giác vuông, vừa là tam giác cân.
Diện tích tam giác thường
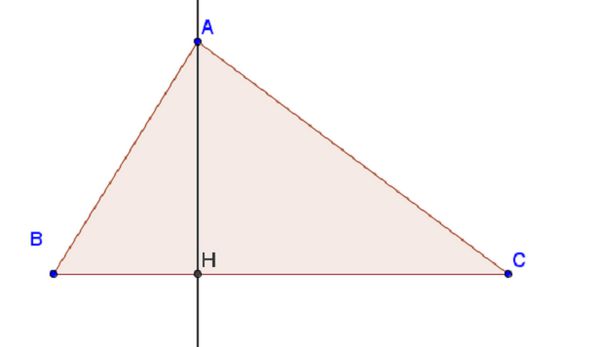
Với: Ta có 1 tam giác ABC có ba cạnh a, b, c, ha là đường cao từ đỉnh A
a. Công thức tính chung
– Diện tích tam giác bằng ½ tích của chiều cao hạ từ đỉnh với độ dài cạnh đối diện của đỉnh.
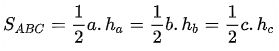
b. Diện tích tam giác khi biết 1 góc
– Diện tích tam giác bằng ½ tích hai cạnh kề với sin của góc hợp bởi hai cạnh đó trong tam giác.
![]()
c. Diện tích tam giác khi biết 3 cạnh bằng công thức Heron.
![]()
Với p là nửa chu vi tam giác
![]()
Ta có thể viết lại:
![]()
d. Diện tích bằng bán kính đường tròn ngoại tiếp tam giác (R)
![]()
e. Diện tích bằng bán kính đường tròn nội tiếp tam giác (r)
![]()
Diện tích tam giác cân
Với:
– a là độ dài cạnh đáy.
– b là độ dài hai cạnh bên.
– ha là đường cao từ đỉnh A.
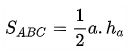
Diện tích tam giác điều
Với:
– a là độ dài các cạnh.
![]()
Diện tích tam giác vuông
Với:
– Tam giác ABC vuông tại B.
– a, b là độ dài hai cạnh góc vuông.
![]()
Diện tích tam giác vuông cân
Với:
– Tam giác ABC vuông cân tại A.
– a là độ dài hai cạnh góc vuông.
![]()
Công thức tính chu vi hình tam giác
Chu vi tam giác thường
Công thức: P = a + b + c
Trong đó:
– P là chu vi tam giác.
– a, b, c là 3 cạnh của hình tam giác.
Từ đó, chúng ta có công thức tính nữa chu vi tam giác thường như sau:
Công thức: 1/2 P = (a+b+c)/2
Chu vi tam giác vuông
Công thức: P= a + b + c
Trong đó:
– a và b : Hai cạnh của tam giác vuông.
– c là cạnh huyền của tam giác vuông.
Chu vi tam giác cân
Công thức: P = 2 a + c
Trong đó:
– a : Hai cạnh bên của tam giác cân.
– c là đáy của tam giác.
Chu vi tam giác điều
Công thức: P = 3 x a
Trong đó:
– P là chu vi tam giác đều.
– a là chiều dài cạnh của tam giác.
Với từng trường hợp cụ thể, mà chúng ta sẽ có các công thức tính chu vi và diện tích của một tam giác bất kỳ để áp dụng vào việc tính toán cho từng bài toán cụ thể.